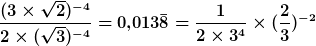Potenzgesetze
Die Potenzgesetze sind mathematische Regeln, die es ermöglichen, Potenzterme, die einem bestimmten Schema folgen, umzustellen, um etwa Rechenarbeit zu erleichtern oder Termumformungen durchzuführen.
Die formalen Regeln
Mithilfe der formalen Regeln kann jede Herausforderung im Bezug auf „Potenzwirrwar“ gemeistert werden. Für Schüler ist gerade diese formale Definition ein gutes Training, um auch in einem späteren Studium kompliziertere Formeln benutzen zu können.
Tipp: Die Buchstaben müssen nur durch eine immer gleiche Zahl ersetzt werden.
Die Regeln direkt
Multiplikation von Potenzen
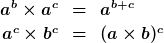
Division von Potenzen
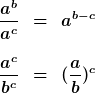
Addition und Subtraktion von Potenzen
Achtung! Dafür gibt es keine Regeln! Derartige Operationen sind nichts anderes als FALSCH!
Potenzieren von Potenzen
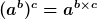
Radizieren von Potenzen
![\sqrt[c]<a^b> = (a^b)^<\frac<1><c>> = a^<b\times\frac<1><c>>=a^\frac<b><c> \sqrt[c]<a^b> = (a^b)^<\frac<1><c>> = a^<b\times\frac<1><c>>=a^\frac<b><c>](/lib/exe/fetch.php?hash=071a61&media=http%3A%2F%2Fapps.rkcsd.com%2Flatex2png.php%2F%255Csqrt%255Bc%255D%257Ba%255Eb%257D%2520%3D%2520%2528a%255Eb%2529%255E%257B%255Cfrac%257B1%257D%257Bc%257D%257D%2520%3D%2520a%255E%257Bb%255Ctimes%255Cfrac%257B1%257D%257Bc%257D%257D%3Da%255E%255Cfrac%257Bb%257D%257Bc%257D.png)
Tipp: Wenn man die Definitionen unter “Sonstiges“ bedenkt, bemerkt man, dass aus dieser Regel auch 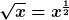 beziehungsweise
beziehungsweise ![\sqrt[n]<x>=x^\frac<1><n> \sqrt[n]<x>=x^\frac<1><n>](/lib/exe/fetch.php?hash=75a4a0&media=http%3A%2F%2Fapps.rkcsd.com%2Flatex2png.php%2F%255Csqrt%255Bn%255D%257Bx%257D%3Dx%255E%255Cfrac%257B1%257D%257Bn%257D.png) folgt.
folgt.
Sonstiges

Bemerkung für Schüler: Die in der letzten Zeile aufgeführte Definition stellt üblicherweise kein notwendiges Wissen für Abschlussklausuren dar. Hier sind allerdings ausdrücklich die unterschiedlichen Regelungen in Bundesländern und Schulformen zu beachten, diese Angabe ist selbstverständlich ohne Gewähr.
Download
Ein Infoblatt zu den formalen Regeln ist hier auch als PDF-Datei verfügbar.
Ein Beispiel
Aufgabe:
Vereinfachen Sie mithilfe der bekannten Potenzgesetze so weit wie möglich!
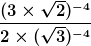
Lösung:
Schritt 1: Die Wurzeln werden in Potenzen umgewandelt, siehe “Radizieren von Potenzen“.
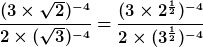
Schritt 2: Die Klammer im Zähler wird aufgelöst, siehe “Multiplikation von Potenzen“, und die Schreibweise im Nenner etwas angepasst, ohne dort jedoch Rechenschritte vorzunehmen.
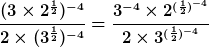
Schritt 3: Der Bruch wird „getrennt“. (Ja, das darf man so machen ![]() )
)
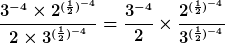
Schritt 4: Die Exponenten im zweiten Faktor werden gemäß “Potenzieren von Potenzen“ zusammengefasst.
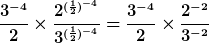
Schritt 5: Jetzt muss man wissen, dass 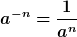 bei
bei 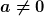 ist. Damit können wir den ersten Faktor umformen.
ist. Damit können wir den ersten Faktor umformen.
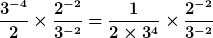
Schritt 6: Zum Schluss arbeiten wir bei dem zweiten Faktor noch mit der Regel “Division von Potenzen“ und sind in der einfachst möglichen Form – oder? Selber Nachdenken macht schlau!
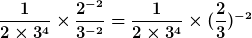
Korrektur:
Richtig gerechnet!