Investitionsentscheidungen
Dieser Artikel ist eine, keinen Anspruch auf Vollständigkeit erhebende, Zusammenstellung einiger wesentlicher Methoden der Betriebswirtschaftslehre, was die Beurteilung der Vorteilhaftigkeit von Investitionen bzw. die Investitionsrechnung/Entscheidungsfindung angeht.
Aufzinsung & Abzinsung
Bei einer Aufzinsung zinst man einen gegebenen Anfangsbetrag 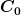 bei einem gegebenen Zinssatz
bei einem gegebenen Zinssatz  auf den entsprechenden Geldwert der letzten Periode
auf den entsprechenden Geldwert der letzten Periode 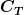 auf.
auf.
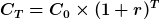
Bei einer Abzinsung zinst man einen gegebenen Endbetrag 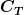 bei einem gegebenen Zinssatz
bei einem gegebenen Zinssatz  auf den entsprechenden Geldwert der ersten Periode
auf den entsprechenden Geldwert der ersten Periode 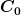 ab.
ab.
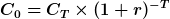
Diese beiden Operationen invertieren sich gegenseitig. Sie dienen dazu, Geldwerte bzw. Zahlungen zu verschiedenen Zeitpunkten vergleichbar zu machen, indem ihr Wert auf einen übereinstimmenden Bezugszeitpunkt umgerechnet wird.
Falls der Hintergrund hierzu nicht unmittelbar einleuchtet: Unter der Annahme eines bestehenden Finanzmarktes ist es ja möglich, Kredite aufzunehmen oder Geld anzulegen. Bezüglich der Zinsen ist es also so, dass etwa angelegtes Geld „mehr wird“. Genauso muss man eben auch für aufgenommene Mittel Zinsen zahlen. Daher sind fünf Euro heute nicht Betragmäßig vergleichbar mit 5 Euro in einem Monat. Denn auf meine fünf Euro heute würde ich ja Zinsen bekommen, sodass ich im nächsten Monat entsprechend mehr Geld habe. Die fünf Euro im nächsten Monat sind heute nur 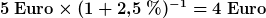 wert, also einen Euro weniger, als die fünf Euro von heute. (Abzinsung). Umgekehrt sind die fünf Euro von heute in einem Monat
wert, also einen Euro weniger, als die fünf Euro von heute. (Abzinsung). Umgekehrt sind die fünf Euro von heute in einem Monat 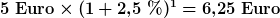 wert (Aufzinsung). Fünf Euro heute oder fünf Euro in einem Monat machen also, zumindest wenn man von Zinsen (hier
wert (Aufzinsung). Fünf Euro heute oder fünf Euro in einem Monat machen also, zumindest wenn man von Zinsen (hier 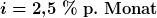 ) ausgeht, einen „gewaltigen“ Unterschied.1)
) ausgeht, einen „gewaltigen“ Unterschied.1)
Rentenrechnung
Eine Rente ist eine Reihe mindestens zwei gleich hoher Zahlungen zu verschiedenen Zeitpunkten (bei gleichem Zeitabstand). Der Rentenbarwert ist nichts anderes, als die Barwerte aller Rentenzahlungen (abgezinst auf 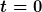 ).
).
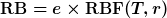
Der Rentenbarwertfaktor ist der Faktor, mit dem ein Rentenbetrag multipliziert werden muss, um den Barwert der Rente zu erhalten.
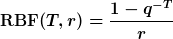
Beispiel:
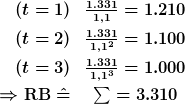
Der Rentenbarwert ist also der Betrag, den wir im Zeitpunkt 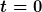 zur Verfügung haben müssten, damit wir aus der Anlage dieses Betrages uns exakt die zu bewertende Rente selber auszahlen könnten und das Konto am Ende geräumt (
zur Verfügung haben müssten, damit wir aus der Anlage dieses Betrages uns exakt die zu bewertende Rente selber auszahlen könnten und das Konto am Ende geräumt (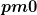 ) ist.
) ist.
Beispiel:
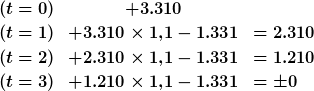
Annuitätenrechnung
Annuitätenrechnung ist die Umkehrrechnung zur Rentenrechnung. Ein einmaliger Betrag wird in eine Rente umgerechnet/ein Ausgangsbetrag wird verrentet.
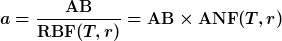
Der entsprechende Annuitätenfaktor lautet:
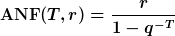
Die äquivalente Annuität
Die äquivalente Annuität 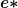 ist dazu da, statt einer zeitpunktbezogenen Kenngröße, eine zeitraumbezogene Kenngröße zur Beurteilung der Vorteilhaftigkeit von Investitionen zu haben. In der betrieblichen Praxis arbeitet man ja schließlich auch eher mit z.B. jährlichen Erfolgsgrößen. Es gilt folgende allgemeine Formel für
ist dazu da, statt einer zeitpunktbezogenen Kenngröße, eine zeitraumbezogene Kenngröße zur Beurteilung der Vorteilhaftigkeit von Investitionen zu haben. In der betrieblichen Praxis arbeitet man ja schließlich auch eher mit z.B. jährlichen Erfolgsgrößen. Es gilt folgende allgemeine Formel für 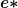 :
:
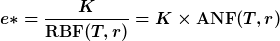
Sprich: „Die Annuität eines Investitionsprojektes entspricht dem verrenteten Kapitalwert.“
Endwert
Der Endwert einer Investition gibt an, ob das (eingesetzte) Vermögen des Investors im Vergleich zur Unterlassungsalternative nach Ende des Investitionsprojektes höher oder niedriger ist.
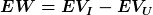
Berechnung:
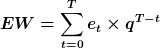
Kapitalwert
Der Kapitalwert ist der über die Investitionsprojektlaufzeit abgezinste Endwert. Der Endwert ist der über die Laufzeit aufgezinste Kapitalwert.
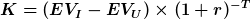
Um den Kapitalwert einer gegebenen Zahlungsreihe zu berechnen, kann man die Kapitalwertmethode verwenden.
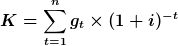
Für die Beispielzahlungsreihe 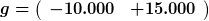 ergäbe sich also (bei einem Zinssatz von
ergäbe sich also (bei einem Zinssatz von 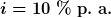 ):
):
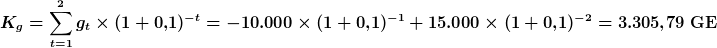
Die ökonomische Interpretation des Ergebnisses ist, dass sich die betreffende Investition lohnt, da der Kapitalwert positiv ist. Sie ist der sogenannten Unterlassensalternative vorzuziehen.
Kapitalbindung
Kapitalbindung rechnet man mit folgender Formel aus:
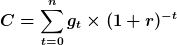
Auswahlentscheidungen
Bei projektindividuellen Entscheidungen gelten die drei Prämissen
- nur Projekte durchzuführen, die ein höhres Endvermögen als die Unterlassungsalternative haben,
- nur Projekte durchzuführen, deren Endwert positiv ist und
- nur Projekte durchzuführen, deren Kapitalwert positiv ist.
Bei Auswahlentscheidungen ist die Sache u.U. anders: Die entsprechenden Kennziffern 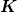 bzw.
bzw. 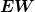 sind nur dann vergleichbar, wenn sie sich auf den gleichen Zeitpunkt beziehen. Bei
sind nur dann vergleichbar, wenn sie sich auf den gleichen Zeitpunkt beziehen. Bei 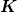 ist das natürlich der Fall, da die Werte ja auf den Zeitpunkt
ist das natürlich der Fall, da die Werte ja auf den Zeitpunkt 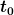 abgezinst werden. Bei dem Endwert jedoch wird ja der Wert am Ende der Laufzeit berechnet, und die Laufzeiten verschiedener Projekte unterscheiden sich ja gegebenenfalls.
abgezinst werden. Bei dem Endwert jedoch wird ja der Wert am Ende der Laufzeit berechnet, und die Laufzeiten verschiedener Projekte unterscheiden sich ja gegebenenfalls.
Differenzzahlungsreihe
Mit der Differenzzahlungsreihe kann man die relative Vorteilhaftigkeit von Investitionen gegenüber einander beurteilen. Es sind jedoch keine Aussagen darüber möglich, ob bspw. lieber die Unterlassungsalternative aller in Betracht gezogenen Investitionsprojekten vorgezogen werden sollte, weil sie sich, auf deutsch gesagt, alle nicht lohnen.
Der interne Zinsfuß
Der interne Zinsfuß 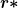 ist der Zins, zu dem die Kapitalwertfunktion genau den Wert 0 annimmt.
ist der Zins, zu dem die Kapitalwertfunktion genau den Wert 0 annimmt.