Lagemaße
Was in der Umgangssprache schlicht der „Durschnitt“ ist, erfordert in der Welt der Statistik mehr als „Durschnittswissen“, ist allerdings Standardwissen. ![]() Lagemaße sind Mittelwerte; etwas, das mithilfe einer einzigen charakteristischen Größe alle beobachteten (Merkmals-)Werte möglichst gut repräsentiert.
Lagemaße sind Mittelwerte; etwas, das mithilfe einer einzigen charakteristischen Größe alle beobachteten (Merkmals-)Werte möglichst gut repräsentiert.
Modalwert
Der Modalwert  einer Verteilung (= Menge der beobachteten Werte), auch als Modus bezeichnet, ist der Wert, der am häufigsten vorkommt, also
einer Verteilung (= Menge der beobachteten Werte), auch als Modus bezeichnet, ist der Wert, der am häufigsten vorkommt, also  . Im fall von nominal Skalierten Merkmalen kann nur der Modalwert als sinnvolles Lagemaß benutzt werden.
. Im fall von nominal Skalierten Merkmalen kann nur der Modalwert als sinnvolles Lagemaß benutzt werden.
Median
Der Median 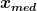 kann nur verwendet werden, wenn die Werte wenigstens Ordinalskaliert sind. Die Werte müssen unbedingt entsprechend sortiert werden, bevor der Median gebildet werden kann!
kann nur verwendet werden, wenn die Werte wenigstens Ordinalskaliert sind. Die Werte müssen unbedingt entsprechend sortiert werden, bevor der Median gebildet werden kann!
Entsprechend wird eine geordnete Reihe von Werten betrachtet. Der Wert, der bei dieser Reihe in der Mitte steht, ist dann der Median:
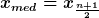
Das geht natürlich nur bei einer ungeraden Zahl von Elementen.
Wenn die Zahl gerade ist, wird der Mittelwert, genauer gesagt das arithmetische Mittel (siehe unten), von den beiden Werten in der Mitte gebildet:

Arithmetisches Mittel
Das aritmetische Mittel 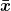 ist das, was man im Allgemeinen auch unter dem umgangssprachlichen Durchschnitt versteht:
ist das, was man im Allgemeinen auch unter dem umgangssprachlichen Durchschnitt versteht:
Es handelt sich ganz genau genommen um das ungewogene arithmetische Mittel.
Gewogenes arithmetisches Mittel
Das gewogene arithmetische Mittel 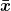 berücksigtigt im Gegensatz zum ungewogenen die häufigkeiten der Beobachtungen. In der folgenden mathematischen Definition steht
berücksigtigt im Gegensatz zum ungewogenen die häufigkeiten der Beobachtungen. In der folgenden mathematischen Definition steht 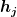 für die absoluten und
für die absoluten und 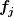 für die relativen Häufigkeiten!
für die relativen Häufigkeiten!
Das  „relativiert“ letztendlich einfach nur die absoluten Werte.
„relativiert“ letztendlich einfach nur die absoluten Werte.
Um das gewogene aritmetische Mittel etwas deutlicher zu machen folgendes Beispiel: Man will die durchschnittliche Zahl an Kunden, die täglich ein Geschäft betreten, berechnen. Wenn die Zahlen als Wertereihe vorliegen, kann man mit dem ungewogenen arithmetischen Mittel arbeiten. Hat man jedoch zusammenfassende Werte wie „an 5 Tagen waren jeweils 18 Kunden“ und „an 3 Tagen waren je 22 Kunden im Laden“ ist das gewogene arithmetische Mittel zu verwenden. Hier die Rechnung, die auch die oben stehende Formel erläutert:
Es waren also „durchschittlich“ 19,5 Personen in dem Laden an den acht Tagen. Im Prinzip ist das gewogene arithmetische Mittel sowas wie das „zusammengefasste ungewogene arithmetische Mittel“. Denn man könnte das auch umständlich mit dem aritmetischen Mittel ausrechnen:
Geometrisches Mittel
Das geometrische Mittel wird benötigt, um etwa durchschnittliche prozentuale Veränderungen, etwa bei Zinsen, zu berechnen. Dies ist mit dem aritmetischen Mittel nicht möglich.
Ein Beispiel: Es wird ein Betrag von 1.000 Geldeinheiten über fünf Jahre angelegt. Im ersten Jahr erhalten wir 2 % Zinsen und in jedem weiteren Jahr ein Prozent mehr.
Nach den fünf Jahren haben wir also einen Betrag von 216,09 GE als Zinsen erhalten. Wenn wir das einfacher rechnen möchten, kann man die durchschnittliche prozentuale Veränderung nehmen und für die fünf Jahre rechnen. Wenn man dies mit dem arithmetischen Mittel ausrechnen würde, käme etwas falsches heraus:
Die Verwendung des geometrischen Mittels führt jedoch zu einem richtigen Ergebnis:
Ganz wichtig: Hier durften keinesfalls die Prozentwerte eingesetzt werden, sondern es muss mit den Faktoren gerechnet werden, um zu einem korrekten Ergebnis zu kommen!
Wird nun mit diesem Faktor bzw. Durschnittszinssatz gerechnet, gelangt man zu dem korrekten Endkapitalbetrag:
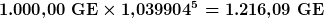
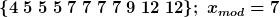
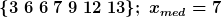
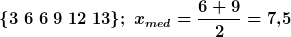
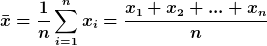


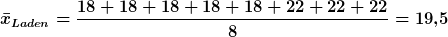
![\bar<x>_<geom>=\sqrt[n]<x_1\times x_2\times...\times x_n>=\sqrt[n]<\prod_<i=1>^<n>x_i> \bar<x>_<geom>=\sqrt[n]<x_1\times x_2\times...\times x_n>=\sqrt[n]<\prod_<i=1>^<n>x_i>](/lib/exe/fetch.php?hash=75911d&media=http%3A%2F%2Fapps.rkcsd.com%2Flatex2png.php%2F%255Cbar%257Bx%257D_%257Bgeom%257D%3D%255Csqrt%255Bn%255D%257Bx_1%255Ctimes%2520x_2%255Ctimes...%255Ctimes%2520x_n%257D%3D%255Csqrt%255Bn%255D%257B%255Cprod_%257Bi%3D1%257D%255E%257Bn%257Dx_i%257D.png)
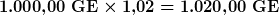


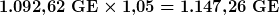
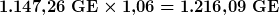
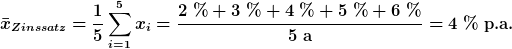
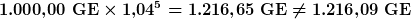
![\bar<x>_<Zinssatz>=\sqrt[5]<\prod_<i=1>^<5>x_i>=\sqrt[5~\textbf<a>]<1<,>02\times1<,>03\times1<,>04\times1<,>05\times1<,>06>\approx3<,>9904~%25~\textbf<p.a.> \bar<x>_<Zinssatz>=\sqrt[5]<\prod_<i=1>^<5>x_i>=\sqrt[5~\textbf<a>]<1<,>02\times1<,>03\times1<,>04\times1<,>05\times1<,>06>\approx3<,>9904~%25~\textbf<p.a.>](/lib/exe/fetch.php?hash=ff5524&media=http%3A%2F%2Fapps.rkcsd.com%2Flatex2png.php%2F%255Cbar%257Bx%257D_%257BZinssatz%257D%3D%255Csqrt%255B5%255D%257B%255Cprod_%257Bi%3D1%257D%255E%257B5%257Dx_i%257D%3D%255Csqrt%255B5~%255Ctextbf%257Ba%257D%255D%257B1%257B%2C%257D02%255Ctimes1%257B%2C%257D03%255Ctimes1%257B%2C%257D04%255Ctimes1%257B%2C%257D05%255Ctimes1%257B%2C%257D06%257D%255Capprox3%257B%2C%257D9904~%2525~%255Ctextbf%257Bp.a.%257D.png)
![\bar<x>_<geom>=\sqrt[n]<x_1^<h_1>\times x_2^<h_2>\times...\times x_n^<h_m>>=\sqrt[n]<\prod_<j=1>^<m>x_j^<h_j>>=\prod_<j=1>^<m>x_j^<f_j>.png \bar<x>_<geom>=\sqrt[n]<x_1^<h_1>\times x_2^<h_2>\times...\times x_n^<h_m>>=\sqrt[n]<\prod_<j=1>^<m>x_j^<h_j>>=\prod_<j=1>^<m>x_j^<f_j>.png](/lib/exe/fetch.php?hash=a6545d&media=http%3A%2F%2Fapps.rkcsd.com%2Flatex2png.php%2F%255Cbar%257Bx%257D_%257Bgeom%257D%3D%255Csqrt%255Bn%255D%257Bx_1%255E%257Bh_1%257D%255Ctimes%2520x_2%255E%257Bh_2%257D%255Ctimes...%255Ctimes%2520x_n%255E%257Bh_m%257D%257D%3D%255Csqrt%255Bn%255D%257B%255Cprod_%257Bj%3D1%257D%255E%257Bm%257Dx_j%255E%257Bh_j%257D%257D%3D%255Cprod_%257Bj%3D1%257D%255E%257Bm%257Dx_j%255E%257Bf_j%257D.png)