Systematische Kurvendiskussion
Es ist möglich, diesen Artikel als PDF-Fassung herunterzuladen.
Metadaten-Bestimmung
Es wird der natürliche Definitionsbereich 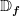 bestimmt.
bestimmt.
Beispiel: 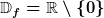 (definiert für alle rellen Zahlen außer 0)
(definiert für alle rellen Zahlen außer 0)
Es wird festgestellt, ob die Funktion stetig ist und bspw. im Falle einer gebrochen-rationalen Funktion beliebig differenzierbar ist.
Ableitungen
Es werden die (ersten drei) Ableitungen der Funktion gebildet.
Beispiel:
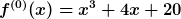
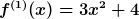
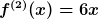
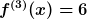
Bemerkung:
Die Schreibweise mit der hochgestellten Zahl in Klammern ist eine alternative Schreibweise für die Hochkommas und stellt keine Potenz dar. Beispiel: 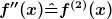
Werte
Es sollte untersucht werden, wie sich die Funktion in Extremsituationen verhält. In unserem Definitionsbereich-Beispiel von oben würde das heißen, dass man untersucht, wie sich die Werte bei gegen 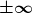 verhalten, sowie bei
verhalten, sowie bei 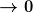 .
.
Nullstellen
Die Nullstellen werden einfach bestimmt, indem die Funktion gleich null gesetzt wird, hier ein einfaches Beispiel:
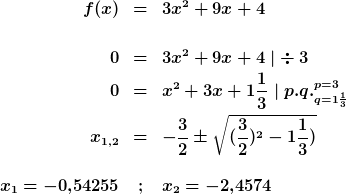
Extrema/Extremwerte
Bedingung für ein Extremum ist, dass das Extrem-x 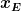 in die erste Ableitung eingesetzt zu
in die erste Ableitung eingesetzt zu 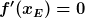 führt. Das ist die notwendige Bedingung. Ob es sich wirklich um Extremstellen handelt, muss dann jedoch noch dadurch geprüft werden, dass man schaut
führt. Das ist die notwendige Bedingung. Ob es sich wirklich um Extremstellen handelt, muss dann jedoch noch dadurch geprüft werden, dass man schaut
- ob die entsprechenden Werte im Definitionsbereich liegen und
- ob die entsprechenden Werte einem Maximum oder einem Minimum entsprechen:
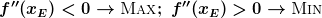
Wenn nicht nur die Werte, sondern auch die Punkte ausgerechnet werden sollen, kann dies ganz einfach durch Einsetzen in die Originalfunktion (nichtabgeleitete Funktion) gemacht werden. Wichtig: Wenn 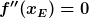 ist, kann keine Aussage über die Art des Extrems gemacht werden.
ist, kann keine Aussage über die Art des Extrems gemacht werden.
Wenn 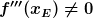 ist, dann liegt keine Extremstelle, sondern eine Sattelstelle vor.
ist, dann liegt keine Extremstelle, sondern eine Sattelstelle vor.
Wendestellen/Wendepunkte
Die notwendige Bedingung zum Vorliegen einer Wendestelle an der Stelle 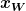 ist
ist 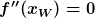 . Die entsprechende Ableitung wird also mit null gleichgesetzt und die Stellen, die am Ende herauskommen, müssen im Definitionsbereich liegen (hinreichende Bed.), dann sind es die Wendestellen. Zur Berechnung entsprechener Punkte sind diese wieder in die Originalfunktion einzusetzen.
. Die entsprechende Ableitung wird also mit null gleichgesetzt und die Stellen, die am Ende herauskommen, müssen im Definitionsbereich liegen (hinreichende Bed.), dann sind es die Wendestellen. Zur Berechnung entsprechener Punkte sind diese wieder in die Originalfunktion einzusetzen.
Monotonie/Krümmung
Aufgrund der Erkenntnisse aus Abschnitt fünf und sechs wird der Graph in Sektionen eingeteilt, über die Aussagen bezüglich monotonem Steigen/Fallen getroffen werden kann.
Ebenso wird bezüglich der Krümmung verfahren: Entsprechend der Erkenntnisse kann beurteilt werden, wie die Krümmung ist: Für 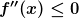 unter der Bedingung das
unter der Bedingung das 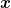 aus dem zu betrachtenden Intervall ist, ist der Graph in diesem Intervall rechtsgekrümmt. Bei
aus dem zu betrachtenden Intervall ist, ist der Graph in diesem Intervall rechtsgekrümmt. Bei 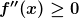 wäre er linksgekrümmt.
wäre er linksgekrümmt.