Inhaltsverzeichnis
Ableitungen
Um Ableitungen der Form
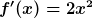
von Funktionen erstellen zu können, werden neben einem „Basis-Prinzip“ fünf Regeln benötigt.
Basisprinzip
Es sei eine Funktion
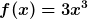
gegeben. Man bildet die erste Ableitung, indem man den Potenzwert mit dem Faktor vor dem 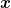 multipliziert. Das Ergebnis wird nun als neuer Faktor vor das
multipliziert. Das Ergebnis wird nun als neuer Faktor vor das 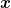 geschrieben und der Potenzwert um eins verringert:
geschrieben und der Potenzwert um eins verringert:
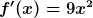
Und so geht das dann als weiter:
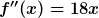
Man beachte, dass im letzten Schritt, das eben schon quasi unsichtbare „hoch eins“ jetzt zur Null wird und daher die dritte Ableitung wie folgt lautet:
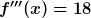
Denn:
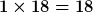 und
und 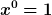
Die fünf Regeln
Faktorregel:
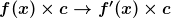
Summenregel:
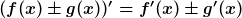
Produktregel:
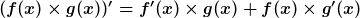
Quotientenregel:
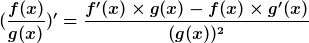
Kettenregel:
![[f(g(x))]' = f'(g(x)) \times g'(x) [f(g(x))]' = f'(g(x)) \times g'(x)](/lib/exe/fetch.php?hash=7ee818&media=http%3A%2F%2Fapps.rkcsd.com%2Flatex2png.php%2F%255Bf%2528g%2528x%2529%2529%255D%255Chk%2520%3D%2520f%255Chk%2528g%2528x%2529%2529%2520%255Ctimes%2520g%255Chk%2528x%2529.png)
Die hier aufgeführten Regeln werden auch als PDF-Dokument angeboten. Siehe auch Integrationsregeln.
Falls nicht anders bezeichnet, ist der Inhalt dieses Wikis unter der folgenden Lizenz veröffentlicht: CC Attribution-Share Alike 3.0 Unported

 2012-2026 René Knipschild |
2012-2026 René Knipschild |