Entscheidungen unter Unsicherheit
Entscheidungen unter Unsicherheit gehören zum unternehmerischen Alltag. Man entscheidet in vielen Fällen nach nicht-zahlenmäßig nennbaren Kriterien, welche Entscheidung man trifft. Die wissenschaftliche Betrachtung setzt soetwas jedoch voraus – beziehungsweise mindestens eine strukturierte Art der Aufbereitung, an der man logisch eine Entscheidung festmachen kann.1)
Grundlagen
Unsicherheitsbedingte Entscheidungsprobleme zeichnen sich durch folgende Eigenschaften aus:
- Es geht immer darum, eine Entscheidung zwischen mehreren, sich gegenseitig ausschließenden Möglichkeiten, sogenannten „Handlungsalternativen“, zu treffen.
- Es ist nicht sicher, zu welchem Ende die jeweiligen Alternativen führen. Dies ist von zusätzlichen Faktoren abhängig.
- Diese Faktoren sind etweder vom Zufall oder anderen, ebenfalls im Zusammenhang handelnden, Personen abhängig.
- Es besteht stets das Problem, nach welchen Kriterien man eine optimale Entscheidung überhaupt treffen soll.
Das Grundmodell
Die Realität ist zu komplex, um Entscheidungen unter Unsicherheit voll und ganz analysieren zu können, und dementsprechend die optimale Handlungsalternative zu bestimmen. Man bedient sich daher Modellen, die nur einen Ausschnitt der Realität zeigen.
Im Falle der Entscheidungen unter Unsicherheit gibt es drei Komonenten,
- die Handlungsalternativen,
- Umweltzustände und
- Handlungskonsequenzen.
Grundlage des Modells ist die Annahme, dass es eine Menge einnander ausschließenden Handlungsalternativen 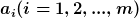 , sowie ergebnisbeeinflussende Umweltzustände
, sowie ergebnisbeeinflussende Umweltzustände 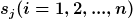 gibt, daraus folgen alle möglichen Ergebnisse, doppeldeutig gemeint:
gibt, daraus folgen alle möglichen Ergebnisse, doppeldeutig gemeint:
Bewertung und charakterisierung von Ergebnisverteilungen
 Fortsetzung folgt…
Fortsetzung folgt… ![]()
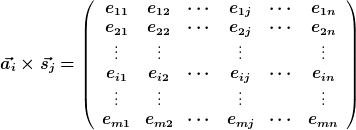

 2012-2025 René Knipschild |
2012-2025 René Knipschild |