Das Konfidenzintervall

Das Konfidenzintervall

Im Rahmen einer statistischen Stichprobe ergibt sich die Problematik, dass nicht mit 100-%-tiger Gewissheit Aussagen über die unbekannte Grundgesamtheit gemacht werden können. Beispiel: Wenn man 1.000 Bundesbürger befragt, kann man damit Aussagen über alle Bundesbürger machen, aber eben nicht mit 100-%-tiger Gewissheit.

Eine Zufallsvariable 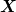nimmt im Rahmen dieser Stichprobe ein bestimmtes Verteilungsmuster an, z.B. die Normalverteilung. 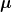$\mu$ ist der Erwartungswert, 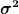$\sigma^2$ die Varianz.

$X \sim N(\mu,\sigma^2)$

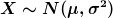
Sprich: 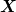ist normalverteilt mit Erwartungswert 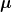$\mu$ (Müh) und Varianz 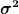$\sigma^2$ (Sigma quadraht).

Erwartungswert & Varianz

Erwartungswert und Varianz berechnen sich je nach Verteilungsart unterschiedlich. Bei der Normalverteilung lauten die Werte einfach:

$E(X)=\mu$
$Var(X)=\sigma^2$

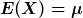
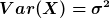
Der Erwartungswert ist der erwartete Wert (wer hätte das gedacht) und die Varianz ist ein Maß für die Streuung der Verteilung um den Erwartungswert.

Beispiel: Standardisieren

Aufgabenstellung

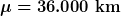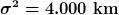Eine Reifenfirma untersucht die Lebensdauer eines neu entwickelten Reifens. Dabei zeigt sich, dass die ermittelte Lebensdauer der Reifen durch eine Normalverteilung mit den Parametern $\mu=36.000~km$ und $\sigma=4.000~km$ angenähert werden kann. Wie groß ist die Wahrscheinlichkeit, dass ein zufällig ausgewählter Reifen höchstens 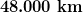hält?

Lösung

Wie aus der Aufgabe hervorgeht, liegt eine Normalverteilung vor.

$X \sim N(\mu = 36.000,\sigma^2 = 4.000^2)$

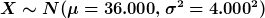
Gesucht ist die Wahrscheinlichkeit dafür, dass die Zufallsvariable 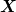einen Wert kleiner oder gleich 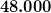48.000 annimmt.

$P(X\leq48.000)$

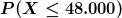
Für die hier vorliegende Normalverteilung findet man Wahrscheinlichkeiten für Zufallswerte in einer entsprechenden Tabelle. Natürlich sind darin nicht alle beliebigen Zahlen enthalten, daher standardisieren wir mit der Formel

$z=\frac<x-\mu><\sigma>$

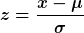
also in unserem Fall

$P(\frac<x-36.000><4.000>) \Leftrightarrow P(\frac<48.000-36.000><4.000>)$

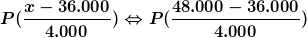
Das Ergebnis des Bruchs, in unserem Fall 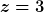z=3 , schauen wir in der Tabelle nach und gelangen zu der Wahrscheinlichkeit, die in der Aufgabe gefragt wurde.

F_Z(3)=0,9987=99,87~%

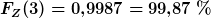
Wir untersuchen also die Wahrscheinlichkeit für ein Ereignis innerhalb des Konfidenzintervalls.

Achtung! Beim Rechnen immer genau schauen ob Sigma quadriert oder nich quadriert ist!

Tipp

Für Statistik-Grundlagenkurse gilt: Die meisten Formelzeichen in der Statistik dienen nur der Verwirrung. Die müssen oftmals nicht ausgerechnet werden, nur ausgeklammert. Doppelte Summen sind nur Tabellen, die zeilen- und spaltenweise addiert werden müssen. Und alles andere ist die richtigen Zahlen in Tabellen nachgucken. Also keine Panik. :-)