Zusammenhangsmaße
Mithilfe von Zusammenhangsmaßen bzw. Korrelationsrechnung wird der lineare Zusammenhang zweier Merkmale einer Verteilung gemessen. Hierbei spielt die Skalierung eine wichtige Rolle, da je nach Skalierung mit einem genaueren Maß gerechnet werden kann bzw. umgekehrt nicht gerechnet werden darf.
Skalierungen
Im Falle lediglich nominal skalierter Merkmale darf der lineare Zusammenhang nur mit der Kontingenz (= Zusammenhang zwischen qualitativen Merkmalen) bzw. dem Kontingenzkoeffizienten berechnet werden. Im Falle ordinalskalierter Merkmale kann die Korrelation (= Zusammenhang zwischen quantitativen/ordinalskalierten Merkmalen) bzw. der Korrelationskoeffizient nach Spearman berechnet werden. Im Falle kardinalskalierter Merkmale wird der Korrelationskoeffizient nach Bravais-Pearson berechnet. Bitte lesen Sie hierzu ggf. den Artikel über Skalierungen aufmerksam durch!
Bitte beachten Sie, dass diese Hierachie rückwärts offen ist, aber nicht vorwärts. Was will uns der Autor mit diesen wirren Worten sagen? Man darf auch von bspw. interwallskalierten Merkmalen einen Kontingenzkoeffizienten ausrechnen. Dieser sagt nur nicht all zu viel aus. Daher sollte man in einem solchen Fall lieber den Bravais-Pearson nehmen. Aber: Man darf zumindest den schwächeren Koeffizienten berechnen. Andersherum gilt dies jedoch nicht! Von nominalskalierten Merkmalen darf der Pearson nicht berechnet werden! Wenn man eine Häufigkeitsverteilung mit verschiedenen Skalierungen zu betrachten hat, muss entsprechend der schwächste Koeffizient verwendet werden, um die Regel nicht zu verletzen.
Korrelationskoeffizient
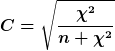
Spearman
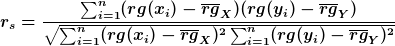
Bravais-Pearson
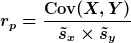

 2012-2025 René Knipschild |
2012-2025 René Knipschild |